El encanto que puede ejercer el numero i es increíble, y es una de las entidades matemáticas más fascinantes que existen. El propósito de esta entrada es conocerlo y comprenderlo con sencillez, pero no falta de profundidad. Así que, ¡manos a la obra!
La definición de i es muy simple, y se expresa como:
\displaystyle i^{2} = -1
¿Por qué esta definición simplona debería sorprendernos? ¡Expliquémoslo!
El fondo de la maravilla: la ley de los signos
¿La recuerdan? Nos dice que si multiplicamos números con el mismo signo obtenemos un resultado positivo, en caso contrario, uno negativo. Así:
\displaystyle \begin{array}{ccc} (+)(+) & = & (+) \\ (+)(-) & = & (-) \\ (-)(+) & = & (-) \\ (-)(-) & = & (+) \end{array}
¿Y qué con eso? Significa que, si multiplicamos un número por sí mismo, como se hace al elevar al cuadrado, el resultado será siempre positivo. Estaremos multiplicando un numero positivo con otro positivo (él mismo), o bien, un negativo con el mismo negativo.
Tiene sentido, ¿no? Es pensar que el negativo de un negativo es un positivo. Algo parecido a negar una negación. Decirle «no» al «no» es «sí». Entonces, ¿cómo es posible que un número multiplicado por sí mismo sea negativo tal cual pasa con i^{2} = -1?
¿Un sinsentido?
Deben pensar que es una frivolidad inventada por alguien sin algo mejor que hacer. Un capricho de la notación, una expresión que se ve bien pero sin significado. Nada más lejos de la verdad. El matemático Gerolamo Cardano lo descubrió cuando intentaba resolver algunas ecuaciones que, durante el procedimiento de su resolución, revelaban números negativos provenientes de una potencia cuadrada. Si utilizaba esos números en el procedimiento (sin saber exactamente qué significaban), al final podía obtener una respuesta común, con números «normales», ¡que era correcta!
Si esas «entidades» permitían encontrar la solución al problema, algo debían significar. Al mismo tiempo eran tan extrañas. Es decir, uno puede imaginar cinco manzanas en una mesa. ¿Pero cómo se ven i manzanas? Tan extravagantes, místicos e irreales parecían, que Rene Descartes terminó por bautizar a i y sus múltiplos como «números imaginarios», y Gottfried Leibniz dijo que \sqrt{-1} era «una especie de anfibio entre el ser y la nada».
Los números complejos
Dada su utilidad práctica, estas entidades extrañas terminaron por incorporarse al corpus matemático y, sumados a los números de siempre, se terminaron por llamar «números complejos». Tales entidades se pueden escribir como la suma de un número «común» conocido como «real», y un número «imaginario». Un ejemplo de número complejo podría ser:
\displaystyle 3 + 4i
Donde 3 es la parte real y 4i la imaginaria. ¡Son como coordenadas! Al menos así los vio alguien y los colocó en un plano que conocemos como plano de Argand, o simplemente, plano complejo.
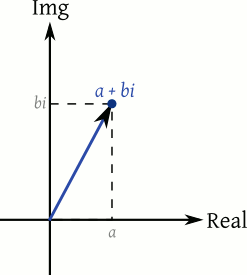
 El número a + bi en el plano complejo.
El número a + bi en el plano complejo.¿Esto no amplía nuestro entendimiento de los números? Han terminado por rebelarse y mostrar su amplia naturaleza, que va más allá de los límites impuestos por la recta numérica que conocemos desde hace tanto tiempo. No viven en una recóndita y escondida línea, atrapados dentro de sus fronteras unidimensionales uno detrás de otro. Por el contrario, se expresan en múltiples dimensiones, danzando y relacionándose en formas más profundas de las que originalmente habíamos intuido.
El número i como una rotación
El número i tiene ciertas propiedades que se desprenden de su definición. Una de las más curiosas es que multiplicar cualquier número por i equivale a rotarlo 90° en el plano complejo.
Por ejemplo, pensemos en el número a + bi. Al multiplicarlo por i queda:
\displaystyle i(a + bi) = ai + bi^{2}
Pero sabemos que i^{2} = -1, por lo tanto, b debe quedar multiplicado por ese factor. Es decir, debe cambiar de signo. Reescribiendo:
ai + bi^{2} = -b + ai
Gráficamente podemos apreciar que esto equivale a rotar el vector original 90°:
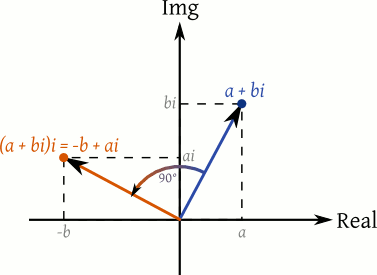
De hecho, se puede obtener una rotación arbitraria de tantos grados como el multiplicador tenga respecto a la recta real.
Belleza visual y abstracta
¿Conocen el conjuntol de Mandelbrot? Seguramente sí, aunque no lo conozcan con ese nombre. Es este:

Y este también, a una escala diferente:

Existe en el plano complejo, y cada punto de color es un número complejo. El proceso que lo crea y las reglas que brindan esos colores tal vez sean abordados en otra entrada de este blog.
Y, ¿existen?
¿Existen los números complejos? Esta pregunta viene de un malentendido sobre aquello que son los números. ¿Existe el cinco o el cuatro? No más ni menos que cualquier número complejo. ¿Por qué entonces es fácil visualizar cinco manzanas, pero no i manzanas? El problema radica, me parece, en creer que los números son cantidades. Ningún número es una cantidad, ninguno. Aunque puedan representarlas perfectamente.
Los números son abstracciones, y no son cosas que existan en el mundo físico, aunque pueden representar acciones y procesos en él. A veces esas representaciones son muy obvias, como sumar manzanas. Sumar números es como juntar manzanas, pero ni las manzanas son números ni los números manzanas. Existe un isomorfismo simple entre la operación suma de los números naturales y juntar muchas manzanas. Así, sin necesidad de juntar manzanas reales, sabemos cuántas tendríamos de amontonar las treinta de Juan y las quince de María. Pero otros procesos no son tan directos, y no hacen alusión a cantidad alguna.
Comentarios finales
El desarrollo de i expandió nuestra mente a un mayor entendimiento de los números y su naturaleza. Uno que trascendió lo que originalmente habíamos concebido para ellos. Este nuevo alcance, esa capacidad de abarcar más de lo que nosotros mismos habíamos imaginado, es la parte más importante de su belleza. Las exquisitas interrelaciones que expresan y nos brindan son su esplendor.



