Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
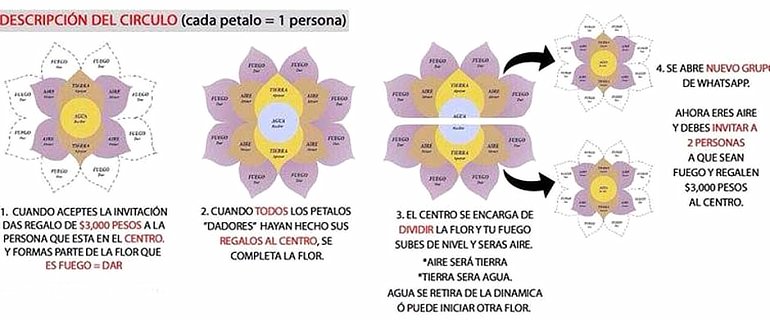
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




Javier, eres un crack. Impecable artículo. Justo me está empezando a rodear este cuento-Ponzi de la flor o el telar y se está difundiendo como epidemia por mi ciudad… no paro de sorprenderme de la ingenuidad y/o de la perversidad de la gente. Unos no ciudan su dinero, otros no tienen escrúpulos en estafar y otros no son capaces de ver que por crédulos o incautos se han convertido en estafadores. Gracias por tu claridad.
Gracias por tus comentarios. ;)
Dejen a la gente creer lo que les plazca,
al fin y al cabo ningun sistema, incluso el bancario, es perfecto…
En este mundo infernal en el que vivimos,
lo que nos queda es probar nuevos mecanismos
para interelacionarnos en todos los niveles.
Más allá de la «impecables» matemáticas,
pienso yo, que es la gente sin confianza en nada más que en lo que se conoce,
aunq no funcione, y mas de medio planeta se muera de hambre,
la que hace fracazar estas alternativas…
¿Pero qué sentido tiene probar lo que YA SABEMOS que no funciona? La desconfianza no es lo que hace fracasar a las flores. Se entiende eso, ¿no?
Bien dicho el riesgo es menor comparado von el beneficio que ningun banco te daria
Que pendejada, y que hay del crecimiento exponencial de la población? Si inviertes de nuevo y nuevas generaciones nacen, en donde está el problema? Claro que se puede sostener el método de la flor, es un método que espanta a muchos pero en realidad ya es usado por muchos.
Contrario a lo que piensas, el problema del crecimiento exponencial es doble: 1) No es lo mismo doblar a los integrantes de las flores cada semana que doblarlos cada varias DÉCADAS (como la población) 2) El crecimiento exponencial de la población es sólo MIENTRAS es sostenible, como la Tierra y sus recursos no son eternos, un día ese crecimiento parará (Y seguramente lo hará de mala manera. Lo que pone a reflexionar sobre nuestra perdición por la legión de personas que ni siquiera puede entender el crecimiento exponencial… como tu).
Por último: ¿cuántas veces hay que repetir que no importa si todos los ganadores reinvierten y que eso no cierra ni arregla nada?
(¿De verdad lo que dices lo haces creyendo en ello? Es ALUCINANTE).
javier estas bn pendejo diario nacen mas 10 millones de personas la población crece mas rapido q la flor
pinche pendejo
crees ser muy listo y ser la verga en vida pero eres un pendejo sin vida sin espectativas
tienes una mentalidad de pobre lo mas seguro es q seas empleado
yo ago este negocio desde hace dos años y no ha caido y con la misma gente yo
grandisimo animal descubri como dar vueltas que las putas matematicas se jodan
Para empezar has de ser de Egipto y allá creen todo esto pero aquí es otra cultura y por lo visto si has estado en esto desde hace mucho entonces eres de los huevones que quieren ganar la vida fácil, y la única manera de ganarse la vida es trabajando, tú como muchos le dan esperanza al jodido, pero todo esto trae un karma y el tuyo ya te llegara porque aunque incluyas a todos los habitantes del mundo alguien va a perder tarde que temprano y la verdad es más temprano que tarde!!! Y no hables con mamadas, le creo más al matemático porque es más congruente que tus razonamientos tercer mundistas. No eres más que un oportunista!
Soy de argentina comunicante conmigo te dejo mi numero 2622412681 y correo fla_flaka@hotmail.com
Supongo que crees que lo que te pasa a ti y a tus amigos es lo que le pasa a todos los que se involucran con ustedes, pues… craso error. Lo que es no saber sumar.
¿Qué más puedo decir de ti que tu ortografía y modales no digan por sí mismos?
Hola me puedes dar informacion por favor
Buenos dias, me parecen excelentes sus articulos . Me han enviado este video de otra flor, quisiera de favor que lo checara y diera su punto de vista, por que este es con solo una inversión de $50 pesos. E igual dice que se puede trabajar no por personas por que se pueden acabar, si no por inversiones, cada persona puede meterse varias veces con una inversión. Me llama la atención esta flor por que son solo 50 pesos los que tu metes. Y si pierdes, son los unicos qje perderias. No miles y miles. Valdra la pena intentarlo? https://youtu.be/qHcbTBnnQ4k
El video que pones es una obscenidad. Te lo explico muy brevemente. Es muy sencillo:
Como el dinero no se crea ni sale de la nada, reflexiona en la cantidad de gente que esta financiando al que «gana» en la flor de $1000. Como es fácil contar, son 20 personas. Cuando llegas a la flor donde pagan $1000, ya juntaste atrás de ti a 20 personas que dieron $50 cada una. Ay de ellos, donde CADA UNO tiene que juntar a sus propias 20 personas para «ganar» igual. Y así ad infinitum.
Simplemente se pierde poco dinero, pero el porcentaje de perdedores es mucho más alto. Todo el resto del discurso son técnicas para encubrir ese hecho.
Esta es una verdad universal y aplica para CUALQUIER sistema piramidal: Las personas nunca alcanzan, el sistema siempre tiene personas a las que se les debe dinero, en ningún momento deja de haber personas a las que se les deba dinero (¿Te has dado cuenta que SIEMPRE se le debe a alguien y que nunca puede existir un momento en que no se deba a nadie?). Además, el número de personas a las que se les debe siempre crece con el tiempo y siempre crece más rápido que los ganadores, como las cosas no son eternas, un día a los que les deben se quedarán así: con pérdida.
Como las flores no fracasan todas a la vez, los perdedores se reparten a lo largo del tiempo, pero siempre existen. Y siempre son MUCHOS. Aproximadamente 7 veces más que los ganadores., y en el esquema del video que me pones son estratosféricamente más (aunque la pérdida es más pequeña. Un tipo de «robo hormiga»).
Un análisis muy claro. Básicamente es una cadena de saqueos. Se aprovechan de la necesidad e ignorancia de la gente, les estimulan sus emociones y sentimientos para que acepten entrar.
Muchas felicidades, muy buen análisis.
por lo que me e informado en realidad este esquema piramidal representa en una forma simplificada y mas acelerada al sistema económico actual ya que estos funcionan con un crecimiento exponencial y los dos se alimenta de las personas que pierden.
Cuando alguien se atreve hablar de algo que no conoce y afirmar que es un fraude, es muy probable que el fraude este en su misma persona. Por que cada uno es lo que expresa o vive. Yo puedo dar mi testimonio que esto realmente funciona, en medida que cada quien tome su responsabilidad, cada persona ingresa con dos nuevas y obvio existe el reciclaje, no necesariamente tiene que ser nueva, nueva. miles de personas sean beneficiado con telares, flores, y obvio al nuestro sistema en el cual vivimos no le conviene. por eso la mala información.
¿En qué parte del artículo dice que es un fraude?
Por otro lado, si tu testimonio es que has ganado y has visto a gente ganar, eso no lo niega nadie, lo que se afirma es que hay más perdedores que ganadores, que eso es matemáticamente inevitable y existen aunque tu no los veas ¿Fácil de entender no?
Es decir, si mil se han beneficiado, siete mil se han perjudicado, y precisamente la alerta está en que eso es difícil de ver.
Cuando alguien que hace un «sistema de abundancia», que no es otra cosa mas que una pirámide Ponzi pero con ciertas variantes y no se ha puesto a leer que esto está penado en más de 50 países en el mundo y se paga con la cárcel al responsable es porque le hace falta muchísimo conocimiento al respecto.
Sí señor, es un FRAUDE por donde le veas.
¿No tienes botón para compartir en Facebook? Si no, bueno, sólo copiaré la URL y la publicaré en mi muro. Tu artículo está GENIAL.
Me invitaron a un telar donde lo conforman el del centro atrás de el otros dos y atrás de ellos otros 4 en total son 7.
Crees q con esa forma c pueda hacer un proceso circular q como vallan saliendo vallan entrando de nuevo y así sucesivamente
Entran siete, pero sólo uno recibe dinero, ¿correcto?
Entonces, el que recibió el dinero entra de nuevo, pero necesita otros seis para volver a entrar, ¿no? En ese caso, que la persona que recibió dinero vuelta a entrar hace una muy pequeña diferencia.
Excelente laburo el que has hecho, es una lastima que por mas explicaciones matematicas que des, mucha gente va a caer en la trampa igual, sobre todo mujeres.
A mucha gente de mi familia le ofrecieron esto, y tan solo mi trabajo es informarles.