Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
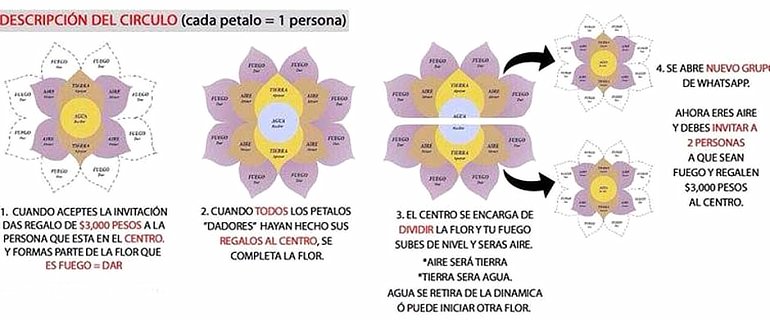
¿En qué consiste la flor?
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




Una duda en que mentó se hace eso ? De bajar la cantidad o en que flor ? Gracias .
En efecto, todos esos modelos económicos piramidales (llamese telares, flor de la abundancia etc) estan destinados al fracaso. Yo entre a uno y tuve que salirme inmediatamente cuando hice las matematicas. Nadie se toma el tiempo de determinar cuando colapsara el sistema. Desgraciadamente el gancho en esos proyectos es que vas a ayudar a alguien y a ti mismo. Y peor son los telares de mujeres, donde te dan un choro mareador de lo bueno que es el proyecto. Te llegan por el corazon y ahi es donde todas caemos.
Cuando hice mis calculos, tomando toda la poblacion mundial (7’500’000,000 aprox) y suponiendo que ABSOLUTAMENTE TODOS (bebes, niños, jovenes, adultos, ancianos) entran con dinero, el sistema colapsa cuando llegan al nivel 28 (la base de la piramide es el nivel 31, pero ya no habra gente abajo que le pague a los niveles 31, 30 y 29), si el telar o la flor, crece un nivel cada semana, en 7 meses habrá colapsado y habrán perdido su dinero 6’562’000,000 de personas. Es decir, los beneficiados con estos sistemas es de tan solo 938’000,000 personas.
Cuiden su dinero, por que cuando entras no tienes idea en que nivel vas, y si estas cerca del colapso, ya te cargo el payaso.
Tampoco hay manera de reciclar a la gente de arriba, porque la piramide crece de manera exponencial, llegara un punto donde todos los que ya hayan recibido su dinero, tendrian que entrar con varios millones de petalos o posiciones al mismo tiempo para salvar un nivel, y despues que?
Matemáticamente (y con un poco de lógica) es imposible creer que este modelo puede sostenerse.
Hola. Se puede hacer alguno parecido a este; que cierto número de personas entren. Un ejemplo que entren 30 personas y que esas personas salga una diaria, para así terminar en un mes , aun que sea menor la cantidad recibida e invertida.
Esa es mi duda. Hacerlo como un «circuito». Que el dinero solo este dando vueltas en esas mismas personas?
No es posible hacer «círculos», precisamente, porque el único dinero disponible en el sistema sería aquel que introducen los participantes. El dinero no aumenta, sólo se redistribuye entre ellos. Si unos ganan, es porque otros pierden (como ya sucede con las flores tradicionales).
Gracias por el artículo, estuve a punto de entrar a una flor solo por quedar bien con otra persona pero gracias a este artículo he salvado mi dinero.
pónganse a trabajar, y dejen de querer ganar dinero fácil,
Si el dinero que fue obtenido por los primeros participantes fueran invertidos en proyectos donde dieran ganacias, podrian esos primeros participantes cerrar la flor o circulo. Talvez en los ultimos participantes no obtengan ganancias(seria algo como un prestamo o su ganancia seria minima) :)
Es bueno que estos artículos develen las patrañas de los esquemas piramidales de estafas. Aún así, muchas personas continuarán hasta que se den cuenta penosamente que han perdido su dinero. Las flores, telares y demás se dejarán en paz por un tiempo y pasado un lapso prudencial regresarán con otros nombres y otros cuentos de economías alternativas y energías cuánticas. Esto nos muestra la terrible necesidad de creer en algo y de la búsqueda de alternativas de financiamiento que el sistema actual tiene cerrados a la mayoría de las personas, lo cual es aprovechado por vivales para cambiar espejitos por oro.
Pues sean peras o manzanas….en la vida siempre habra un riesgo que afrontar en todo proyecto que te propongas……y en este caso dejando a un lado las matematicas y aplicando las probabilidades en este caso puedes ganar aunque sea menos probable que mas probable vemos que aun asi podemos ganar todo depende de ti por que?……por que en este juego si le hechas ganas pasas de ser » victima » a » estafado » recalco si le hechas ganas al fin y al cabo eso si se los aseguro ( personas siempre habra )……bueno mis amigos ya por ultimo les envio una grande felicitacion a todos los ganadores en este sistema y probables perdedores o estafados que Dios los bendiga y los ayude a subir el nivel y logren ganar EXITO PARA TODOS. » SI SE PUEDE «
Cualquiera con un poco de sentido común puede darse cuenta que se trata de un mecanismo destinado al fracaso. Si tal cosa funcionara y la riqueza pudiera generse mágicamente, hace mucho que la humanidad hubiera adoptado este método para que todos nos hiciésemos ricos sin necesidad de ningún esfuezo. Sin embargo no es así. Basta con hacer un sencillo razonamiento: «¿De dónde sale el dinero que va a multiplcar por 8 mi aportación original?» Respuesta: de otros 8 participanetes. ¿Y esos 8 ahora que tienen qué hacer para recuperar su inversión multplicada por 8″ Pues embarcar a 8 cada uno (=64) y, a su vez, esos 64 , cada uno tendrán que encontrar a otros ocho incautos (=512), y así sucesivamente hasta que el sistema reviente y haya mucha, muchísmia gente que perdío exactamente la misma cantidad que los otros ganaron. En otras palabras, se trata de un mecanismo donde no se genera riqueza, sino que se simplemente se pasa de manos Es lo que se conoce como «un juego de suma cero»; donde uno gana otros pierden exactamente en la misma magnitud.
Para que estas cosas funcionen y atrapen a participantes, deben crear la ilusión de que puedes ganar dinero mágicamente y sin esfuerzo. La motivación a participar no es ayudar a nadie, sino beneficiarse rápido y prácticamente sin ningún trabajo. Esa es la base de todos los timos o fraudes, hacer creer a alguien que obtendrá un beneficio fácil. Es un asunto de sicología elemental: se apela a nuestra parte más voraz y egoísta y es entonces cuando, sin pensarlo demasiado, se cometen actos imprudentes.
Yo sólo pido a quien se sienta tentado por estas cosas, que se haga una pregunta: «¿Por qué quiero entrarle, qué es lo que me motiva a participar?» Creo que en el 100% de los casos la respuesta es: «Por que voy a ganar dinero fácil» Después pregúntese si es posible que una cosa aparentemente así de sencilla puede funcionar en verdad y por qué no se le ocurrió a nadie hace ya mucho tiempo.
Hice un código en matlab que gráfica las ecuaciones de la dinámica de este «sistema». Comparto las gráficas:
https://1drv.ms/f/s!An9urix7oLM9rn2Sd707PK3zWrWe
En pocas palabras estas «robando» el dinero de las personas que van a «aportar» y ha inevitablemente perder el suyo.
Si puedes vivir con eso o estas dispuesto a perder tu dinero todo esta bien.