Imagínese una población de lobos y otra de ovejas que cohabitan la misma pradera. Los lobos comen ovejas, y mientras más ovejas comen, más lobos se aparean y reproducen. Claro que llegado un punto, habiendo tantos lobos y tanta necesidad de alimento, las ovejas terminan casi por desaparecer. Al no haber tantas ovejas que comer, la población de lobos empieza a disminuir. Ya no hay comida. Como ahora hay menos depredadores, las ovejas no son masacradas de manera tan rapaz y su población empieza a crecer nuevamente.
Ahora que hay bastantes ovejas, resulta fácil cazarlas, lo que favorece la reproducción de los lobos, y así, ad infinitum, inicia un nuevo ciclo de poblaciones que crecen y disminuyen a ritmos diferentes, el de las presas y los depredadores. Mientras unos florecen, otros decaen.
Este fenómeno, que se da en la naturaleza, es muestra de una de tantas sutiles relaciones que existen entre las diversas poblaciones animales. Por cierto, lo que acabo de enunciar aquí arriba es una descripción cualitativa del fenómeno. Sabemos que el florecimiento de una población está relacionado con el decaimiento de la otra… hasta cierto punto, donde los papeles se invierten.
¿Pero qué punto? ¿Cada cuánto tiempo el ciclo se repite? ¿Se repite siempre igual? Para analizar un fenómeno de esta naturaleza necesitamos algo más que una mera descripción cualitativa del mismo. Necesitamos una descripción cuantitativa. Un modelo.
Descripción cualitativa
El modelo típico (que no el único) de este escenario son las ecuaciones de Lotka-Volterra (1). Un sistema de ecuaciones diferenciales no lineales que pretenden describir la evolución en el tiempo de las poblaciones mencionadas. Las ecuaciones, para los interesados, son las siguientes:
\displaystyle \frac{dx}{dt} = x(\alpha - \beta y)
\displaystyle \frac{dy}{dt} = -y(\gamma - \delta x)
Claro que colocar aquí las ecuaciones es solo para impresionar, ya que no se analizarán en profundidad, ni tampoco se abordará mecanismo alguno de solución. Baste para conocerlas de vista y saber de su existencia.
Las soluciones al sistema se ven más o menos así:
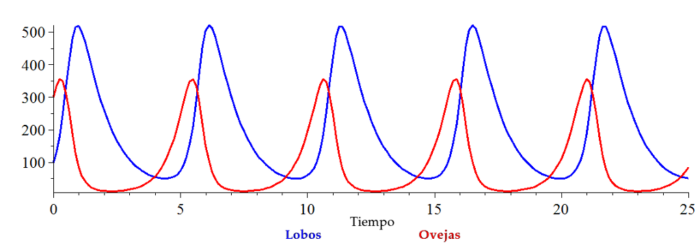
Como es fácil notar el modelo es extremadamente simple y perfectamente predecible, aunque posee características extrañas que no se corresponden con las poblaciones reales. Por ejemplo, que los valores de x e y son continuos y no discretos (2). Como si pudieran existir 100.5 ovejas o 34.3 lobos. Cuando la cantidad de individuos es muy grande, la diferencia que implica agregar o eliminar un individuo no es significativa, y puede ajustar razonablemente bien al modelo. Pero eso no sucede siempre.
También parece dejar a un lado el resto de factores que influyen en el crecimiento o reducción de las poblaciones, como la abundancia o escasez de alimento para las ovejas. El modelo es muy simple, aunque se puede complicar tanto como se desee. En realidad éste en particular no habla de lobos y ovejas, habla de dos entidades abstractas x e y que se relacionan entre sí de cierta manera, y la forma en que varían en función de un valor llamado t (tiempo). Pero así como pueden representar lobos y ovejas, podrían representar sustancias químicas que reaccionan entre sí, o cualquier cosa que se nos ocurra, con tal de que muestren relaciones entre sí similares a las mencionadas.
Complejidad
En la realidad, los depredadores y las presas tienen muchos atributos que van más allá del número de individuos que los componen. Lo animales tienen una posición en el espacio, capacidades físicas y sensoriales diferentes. El terreno que comparten posee límites y características geográficas particulares que podrían alterar el comportamiento de los individuos. Tal vez aquella loma, desde la cual esa pequeña oveja logró divisar a los lobos, la salvó de morir bajo sus filosos dientes, y otras ovejas aprendieron de ella. O simplemente, por selección natural, las ovejas que tienden a comer en dicha loma son las que más se salvan, y al final, la inmensa mayoría de ellas termina haciéndolo. En palabras simples: las interacciones entre los elementos de un sistema pueden ser relevantes para su dinámica.
Al conjunto de disciplinas que se preocupan por la relevancia de las interacciones las conocemos bajo el coloquial nombre de «ciencias de la complejidad». Aquí la palabra «complejidad» posee un significado que la distingue de «complicado». Un sistema puede poseer muchos elementos, lo cual lo vuelve complicado, pero la complejidad radica en lo significativa que puede llegar a ser una interacción, por simple y pequeña que sea. Hace referencia a un sistema en el cual sus componentes como conjunto expresan propiedades que no parecen ser simplemente la suma de las partes individuales. Este concepto está muy emparentado al de «caos» en matemáticas, y ambos tienen muchos ejemplos en común.
Tal vez podría pensarse que, dada una descripción lo suficientemente completa de un fenómeno, sería posible predecir arbitrariamente su comportamiento. Como poner en la ecuación t = 500 y ver el estado de las cosas 500 días en el futuro. Pero este no es el caso necesariamente. Para la inmensa mayoría de las situaciones resulta, no solo difícil, sino imposible hacer predicciones de este tipo sin «echar a andar el modelo», es decir, calcular directamente su evolución y desarrollo durante los 499 días previos para contemplar, ahora sí, lo que ocurre en ese día 500.
A esta característica de los sistemas se le conoce como irreducibilidad computacional, y el concepto surgió de los estudios hechos por Stephen Wolfram sobre autómatas celulares (3) extremadamente simples. Sin entrar en detalles sobre su naturaleza, descubrió que sistemas deterministas con reglas muy sencillas eran capaces de poseer dinámicas ricas y muy complejas (en el sentido descrito anteriormente), imposibles de predecir. Sus reflexiones en torno a este y muchos otros asuntos relacionados, se encuentran expuestas en su muy influyente libro A New Kind of Science, publicado en 2002 (4).
Entonces, ¿a qué recurso podemos apelar para modelar y/o entender la realidad?
Simulación
La ejecución de un modelo arbitrariamente complejo podría recrear las interacciones que de otra forma pasarían desapercibidas. Es decir, una simulación. Tales engendros corren a cargo de instrumentos que hasta hace muy poco tiempo no poseíamos: las computadoras. Ellas son instrumentos que nos permiten ampliar nuestras capacidades. Son como los telescopios que nos permiten observar el cielo y lo muy lejano, o como los microscopios que nos permiten observar lo muy pequeño. Las computadoras son nuevos instrumentos que nos permiten echar una mirada al universo computacional.
Meditemos un poco sobre el asunto: en principio, cualquier cosa, por compleja que sea, es proclive de ser simulada. Tan solo estamos limitados por la velocidad y recursos que la máquina es capaz de emplear. El crecimiento exponencial de sus capacidades a través del tiempo, nos promete un futuro no muy lejano donde seremos capaces de recrear muchas situaciones con gran precisión y detalle. Pronto veremos los efectos de semejantes capacidades en el entendimiento y la predicción de muchos sistemas físicos, biológicos, o incluso sociales, por no hablar de la inteligencia artificial.
En el caso que nos ocupa, podemos simular la dinámica de las poblaciones de presas y depredadores con un modelo muy sencillo, que no por serlo, deja de revelar las sutilezas de esta nueva forma de abordar los problemas. En el ejemplo de abajo se trata simplemente de un terreno cubierto de «pasto», donde vagan libremente «ovejas» y unos cuantos «lobos». Las ovejas comen pasto, que se regenera por sí mismo a cierto ritmo, el cual les permite sobrevivir y reproducirse. Por otro lado, los «lobos» dependen enteramente de su alimentación de ovejas.

Aquí debajo se presenta el resultado de una corrida del modelo:
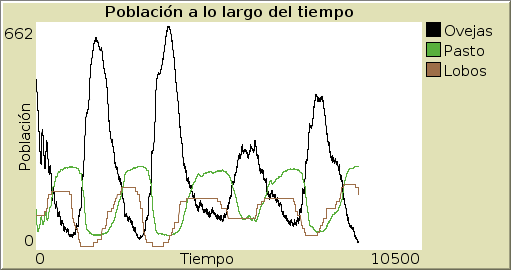
Con toda su sencillez, podemos notar que si bien el comportamiento es cíclico, está lleno de «irregularidades» y fluctuaciones, propias de su naturaleza. Podemos ajustar los parámetros para descubrir fácilmente que no siempre se repiten los ciclos, desembocando todo en la extinción de las especies involucradas, o bien, en la excesiva proliferación de una de ellas.
Para cualquiera que tenga la oportunidad de «jugar» con este pequeñísimo mundo virtual, podrá descubrir que los parámetros iniciales del modelo, por ejemplo, la capacidad de aprovechamiento que las ovejas dan al pasto, o su velocidad de regeneración, casos similares para los lobos, pueden marcar una diferencia muy grande en el comportamiento global del sistema, a pesar de encontrarse dominado por prácticamente las mismas leyes.
No está de más destacar que resulta obvio que los modelos no pueden representar a la realidad hasta sus más pequeños detalles, de lo contrario tendrían que ser la realidad misma, pero sí son capaces de brindarnos la posibilidad de experimentar con realidades que de otra forma serían inaccesibles. Como no son la realidad solo pueden reflejar tendencias y revelar comportamientos altamente probables, según la precisión del modelo. Pero son suficientes para brindarnos nuevos datos con los cuales dar nuevas interpretaciones cualitativas de los fenómenos, y tomar consciencia de cuán sensible puede llegar a ser un sistema a la variación de sus condiciones iniciales y los parámetros que regulan su funcionamiento.
Esta simulación se ha realizado con el modelo proporcionado como ejemplo en el software NetLogo, que puede ser descargado gratuitamente, y que funciona en cualquier plataforma que disponga de una máquina virtual de Java. NetLogo es un entorno programable de modelado multi-agente.
Reflexiones finales
A veces no lo podemos evitar, la falta de información (y capacidad de procesamiento de la misma) nos obliga a ser incapaces de vislumbrar completamente el comportamiento de los sistemas que tenemos delante, o dentro de los cuales nos vemos inmersos nosotros mismos. Por ejemplo, ¿cuantos factores inimaginables para nosotros ahora, marcan la diferencia entre el éxito o el fracaso de tal o cual doctrina económica, o política social, por mucho que suene sensata su exposición a primera vista? ¿Cuántas no se nos han ni siquiera ocurrido? ¿Hasta dónde entendemos la dinámica del mundo que nos rodea?
Algo es seguro: es compleja, y cuanto mayor sea la información que tengamos al respecto mejor la podremos entender. El futuro se nos muestra prometedor debido al indudable crecimiento de nuestras capacidades de cómputo, y lo que ahora son modelos relativamente simples, pronto se volverán monstruosos, permitiéndonos analizar cosas que jamás hubiéramos podido comprender antes.
- Ver Predator-prey model: http://www.scholarpedia.org/article/Predator-prey_model
- El término «discreto» hace referencia a conjuntos de cosas que se pueden contar y ordenar adecuadamente, como los números naturales: 1, 2, 3, etc. En contraste, el término «continuo» hace referencia ineludible a conjuntos infinitos, que además no puedan ser contados ni ordenados. Por ejemplo, todos los números entre 0 y 1.
- Para saber más sobre los autómatas celulares, se puede consultar: https://es.wikipedia.org/wiki/Aut%C3%B3mata_celular
- El libro se puede consultar en línea a través del siguiente enlace: http://www.wolframscience.com/nksonline/toc.html



