Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
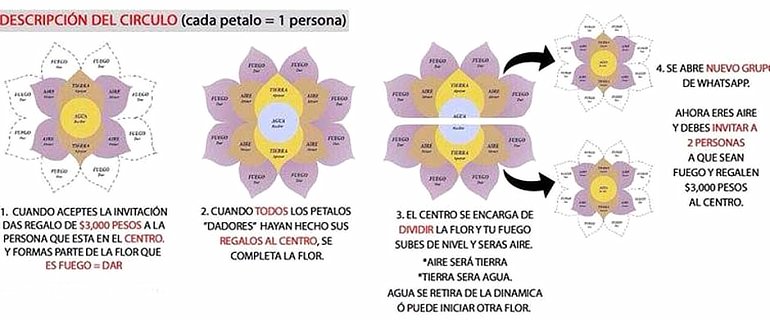
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




Una pregunta, no estoy a favor de este método quiero aclarar, pero acaso no funciona así el sistema bancario? unos ganan mientras otros pierden en mayor o menor medida? no es la manera en que el mundo se mueve? mucho en manos de pocos, y el resto (muchos mas) con poco quienes viven con la «ilusión» de acercarse a ese centro en donde la abundancia es el estilo permanente.
Hola.
La respuesta es no. El sistema bancario no funciona así en lo absoluto, pues la economía no es un sistema de suma cero, como sí lo es la flor de la abundancia.
Por suma cero se entiende que lo que gana uno es la perdida de otro en una relación de 1:1. En la economía, el valor es creado constantemente (Ojo: el VALOR, no el dinero). El valor está sintetizado en los servicios y mercancias que se pueden vender o comprar. Sin nada que vender o comprar, el dinero no vale nada. El dinero tan sólo representa a ese valor. No es valor por sí mismo.
Crear dinero no aumenta el valor que existe en el mundo, porque el dinero no es dicho valor. Si existiera un billete en todo el mundo, él representaría todo el valor existente. Pero si imprimes otro billete, no es que ahora tengas el doble de valor que antes, más bien el valor total se reparte entre esos dos billetes. Por eso imprimir más dinero no hará más rica a la gente.
En la economía «normal», en principio, todos pueden ganar sin que nadie pierda, por la creación de valor implícita en el sistema. Eso es lo que significa «crear riqueza»: llevar a la existencia mercancías o servicios valorados y/o necesitados por la población.
El dinero sí está repartido de forma desigual por el mundo, pero las razones por las que esto es así no tienen nada que ver con la dinámica de la flor de la abundancia.
El sistema de la flor de la abundancia no genera valor en lo absoluto, de ahí que sea de suma cero. Tan sólo es pasar el dinero de unas manos a otras, con la vana esperanza de que ese simple acto lo multiplique mágicamente.
La gente cree que eso de pasar el dinero de unas manos a otras es la economía y por eso se da la confusión que mencionas.
Gracias! Tu explicación me ayudó a entender, me acaban de invitar a algo parecido, ya conocía la base piramidal, y el diamante y no recuerdo qué mas, todas se aprovechan de la gente con sed de dinero, o con necesidades pero que quiere dinero fácil, se dejan engañar, neuro científicamente está comprobado que si uno no está preparado para ver la verdad, se puede maquillar su respuesta y creer lo que se quiere, porque duele saber que debes disciplinarte y trabajar de verdad para potencializar de verdad tu dinero, su valor y sobretodo, administrarlo correctamente. Es un artículo muy valioso! gracias por compartir
Hola! me parece que crear también productos sin necesidad con el simple ímpetu capitalista es muestra de falta de ética y moral, pero si se hiciera un proyecto que a la inversa entra una mayor cantidad de gente y se van cerrando las etapas disminuyendo con ello a las personas, se podría no? así no será infinito
Solo estafan a la gente que viene detrás de los que van capitalizando
Y esos, según tu, ¿qué porcentaje del total de personas es?
Hola Javier, yo estoy en una y he visto que muchos de mis conocidos lo han logrado obtienen su capital, veo matemáticas y esa onda de las manzanas que se lee bonito, mi pregunta es con todo respeto y con el afán de conocer más, tu ya has experimentado en este tipo de sistemas y te ha tocado el colapso de alguno? es que más allá de las matemáticas me gustaría saber en base a tu experiencia donde experimentarse la falla para poder reconsiderar mi participación? Pero lejos de la comprobación numerica, la experiencia que has tenido.
Gracias :)
Mi creencia sincera es que es muy difícil saber de algún colapso si no formas parte de la flor que colapsó, por la sencilla razón de que nadie va a aceptar ante los demás que fue estafado.
Para conocer casos de desesperación, basta ver algunos de los comentarios que aquí mismo han dejado, preguntando cómo salir del embrollo
Velo así: no hay experiencia que vaya a cambiar el hecho de que 2+2=4, o el hecho de que no se pueden repartir más cosas que las que se tienen.
La experiencia, en este caso, hace que algunos, viendo sólo una pequeñísima parte de la imagen completa, crean que quizá el resto de la imagen es como aquello que ellos ven.
Eso es imposible en este caso.
No dudo que haya circunstancias sociales, momentos y lugares que favorezcan mucho el cierre de las flores. Las personas en esas circunstancias sólo conocerán casos de éxito. Pero sólo están viendo una parte (muy pequeña) de todo lo que está sucediendo.
Es una cuestión moral, porque se «gana» siempre a expensas de SIETE perdedores. Siempre. En un contexto donde se miente (por ambición) sobre lo fácil que es perder o ganar, es elección de cada uno arriesgarse, pero también de engañar a los demás.
Excelente artículo, espero que muchas personas lo lean, y lo entiendan de una vez. Pero ya lo dijo Maquiavelo: “El que engaña con arte encuentra siempre gente que se deje engañar”.
Que se deje y hasta implore por ser engañado con tal de no hacerse responsable de sus actos, al final tendrán que responsabilizarse, de todas maneras, pero eso no lo ven en el futuro inmediato. Siempre habrá quien sólo mire como los caballos de desfile, hacia enfrente y no hacia los lados. Como narra platón en el «Mito de las cavernas», salió uno de la caverna, vio el mundo y regresó por los demás y les contó lo que había afuera, pero los demás no podían escuchar todo lo que él decía y se quedaron encerrados en la caverna, o en el libro de «quien se ha llevado mi queso (who moved my cheese)» sucede algo similar