Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
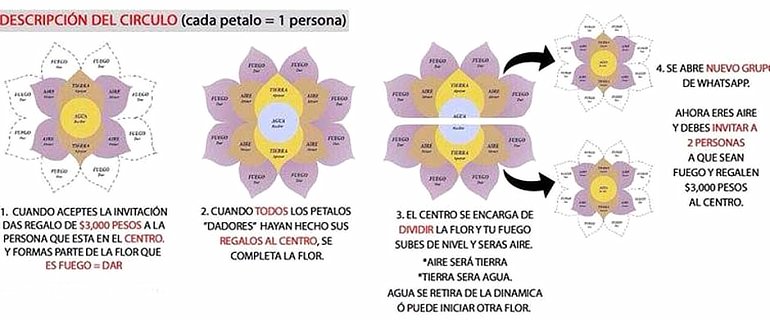
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




No puedo creer que los mexicanos o algun ser humano se deje enbaucar por ese tipo de estafas. Considero q son gente poco inteligente q quiere hacerse rica de la noche a la mañana, si pensaran no entrarian en esas tonterias
Disculpa acavo de leer tu articulo y mi pregunta es si no hay un numero de personas que encapsulen la piramide ,con gente dentro y otros en espera y reduciendolo a tan solo tres niveles o sea 1 , 2 ,4 . Te agradeceria tu respuesta pues mi familia esta poniendose de acuerdo en entrar a uno , y yo no se si es buena idea gracias y asta luego
No hay forma. Sólo es un sistema que mueve el dinero de muchos a las manos de unos pocos. Proporcionalmente son muchos los que pierden y pocos los que ganan. En el caso de la flor tradicional, uno gana y siete pierden.
Hola ami me invita a un juego que es la geometria dinde inviertes 30 pesos y resibes 13 mil pesos en 5 niveles pero disen que ya cuando el primero agarre sus 13 mil en el 5to nivel el juego se ase ciclico quisera saber si se puede o hay una manera para q se aga asi
Nada que dependa de que uno reciba dinero de muchos en estructura piramidal va a funcionar nunca. Solo son sistemas que mueven el dinero de muchos a pocas manos.
Los ganadores siempre son pocos en proporción a los perdedores. SIEMPRE. NO PUEDE SER DE OTRA FORMA.
Hola qyisuera saber porque a mi me invitaron a uno y dicen que cuando ya se junta 3 grupos con 45 personas esta de cierra y va girando los que salen van entrando hasta que pasan todos
Preguntese a si mismo. ¿Es posible «cerrar» una serie flores o telares de forma que no se necesite más gente?
Yo le contesto: ES IMPOSIBLE.
si como los diputados sentados cobrando vibiendo.del pueblo y el puwblo la gwnte cada vez mas.jodida VAMOS A UNIRNOS Y ADIOS A LOS INTERESES DE LOS BANCOS LOS SALAEIOA MISERABLES . BASTA DE DEUDAS
Tienes razón es lo mismo para que como pueblo no podamos pagar nuestras deudas en financieras y bancos y así trabajar pagando puros intereses para que otras personas se alimenten de nuestro trabajo
Es una ironía escandalosa que creas que un sistema que solo mueve el dinero de muchos a unas pocas manos, como los telares, las flores y demás, lo veas como una alternativa a los bancos y los intereses.
Hay alternativas legales para quien invirtió y no recupero?
No que yo sepa, porque se hace a libre voluntad y nadie firma ninguna clase de contrato o compromiso.
Si el «telar» «flor» o como se llame el sistema al que son invitados, es cerrado y se consigue completar el ciclo, déjenme decirles que sería una más de las famosísimas y nunca bien ponderadas TANDAS sólo que con un nombre más atractivo. Y las tandas con gente de confianza funcionan, compruebenlo con su abuela de confianza.
Disculpe todo lo que usted dice si es cierto el detalle es que se en algunos casos se deja un deposita del 10% para cubrir alos demás x si dejase de aver gente y una forma sana es a ser los grupos de 7 personas para k le toque a una de este grupo y por el exceso de gente se puede recortar los grupos en un 80% y el 20% restante seguiría con el trabajo así en un lapso de 2 meses se yegaria a una cantidad de grupos para volver a recortar esa cantidad en un 80% o través y así sería la misma gente que se estaría uniendo al 20% restante en lapsos de 15 días y la gente ya seria segura de que entre y siempre que se le entregue dinero se deja el deposito de 10% lógicamente ay k ver que el organizador sea alguien de la comunidad que tenga su casa y su trabajo ai y que sea un conocido de todos en mi opinión no se si esto es ilegal mientras la gente este de acuerdo y no de queje por que todos ganan también si es ilegal el echo de vender productos de belleza como marcas reconocidas ya seria otra estafa es la misma mecánica siempre lo que se mueve es dinero
No existe forma en que no se necesite siempre más gente. No importan los depositos «por si dejase de haber gente», no importa que se reincorporen los que ya han ganado, no importa recortar nada.
Es IMPOSIBLE. La palabra «IMPOSIBLE» aquí no significa «muy difícil», significa «IMPOSIBLE». Siempre existiran ganadores (una minoria), y siempre existiran perdedores (una mayoría).
Es un sistema que mueve el dinero de muchos a las manos de unos pocos, y resulta una ironía escandalosa que tantos lo vean como una «alternativa» a la economia o los bancos quejándose precisamente por esa razón.
Clarísimo, matemática pura
Que me podría decir acerca del concepto de multinivel, que me han dicho lleva mas de 41 a;os e incluso ya se toma como carrera en algunas universidades de E.U, hay alguna diferencia?
me acaban de invitar a un telar de estos, y entiendo de que se trata, veo que unos ganan que son los que motivan a más gente a entrar, y otros pierden, hay probabilidad de checar la etapa en que va el telar y saber si ganaremos o perderemos ??
Mireya to me hice la misma pregunta que tú, pero por ética se reduce a dos posibilidades esto… A ser estafadora ó ser estafada… Ninguna de las dos me parece justa
No hay probabilidad. Simplemente, es estar al tanto de como van las personas que invitaste, que ellas esten invitando a mas personas. Si en algun momento estando tu dentro y tus dos invitados dentr, alguno de ellos no esta «trabajando» en conseguir a sus dos o estos dos a los que siguen .. la probabilidad de que tu recibas la cantidad multiplicada por los ocho baja. Pero igual el otro invitado hace su trabajo. Tu igual recibes minimo tu invercion mas otras tres.
Hay gente que simplemente no ve más allá de sus narices o sus intereses… como ustedes.
No importa el ánimo, las ganas o el compromiso. Siempre habrá, aproximadamente, 1 ganador por cada 7 perdedores. SIEMPRE.
La decisión ética y moral de entrar jugar, arriesgarse a perder o ganar (siempre a costa de otros) es de cada uno, ciertamente.
Hola he visto muchos ganadores ningún perdedor en tres meses nos ha ido bien a mi e invitados y a sus invitados. quien me ha tocado ver quienes quieren salir por mala información que da alguien que cree tener la razón o no consiguen sus invitados le regresan su dinero, a nadie le interesa defraudar $3,000.00 todo inversionista lleva un riesgo, como nuestro dinero en Afores, en Impuestos que sabemos lo roba gobernantes y funcionarios, en una Tarjeta de Crédito que son altissisimos los intereses y se aprobechan de la mala información que dan para manejarla eso si es abusar de gente, como hay quienes saben utilizarla son muchos mas quienes pasan años pagando interés (creo también puede sacar la proporción matemática sr. javier con muy poco estudio para sacar la formula).
Tengan cuidado cuando los inviten a una flor a muchos conocidos y a mi nos a ido bien no puedo asegurar donde los inviten sean honestos.
Te invito a leer Flores de la abundancia… ¡con manzanas!.
Tal vez así lo veas de otra forma.
Muchas gracias por tu análisis, una amiga quería invertir en uno de estos sistemas y le traté de explicar porque no era posible pero creo que lo hice de una manera muy confusa. Encontré tu artículo y le quedó mucho más claro. Gracias!
Muchas gracias por tu análisis Javier, una amiga quería invertir en uno de estos sistemas y le traté de explicar porque no era buena idea pero creo que lo hice de una manera muy confusa. Le dije que el dinero no se creaba de la nada. Es imposible que sin vender servicios o productos se obtenga una ganancia. Pero creo que tu explicación matemática me ayudo a que entendiera finalmente el funcionamiento de estas estructuras piramidales. Muchas gracias!