Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
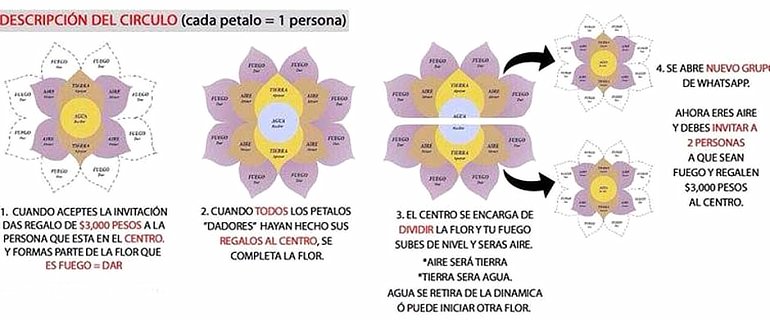
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




Necesito saber si encontraron alguna solucion tengo un telar abierto y no puedo cerrarla
y al final ¿cómo te fue?
Vean la única solución que mi teoría exalta, y puede ayudar a cerrar sin que nadie aparentemente pierda; es que durante el proceso se retenga o se descuente una parte del dinero que van obteniendo los que van ganando, e inviertan en terrenos baldíos o fincas, electrodomésticos u automóviles..en fin….puesto que a la hora de querer cerrar el sistema, se pueda distribuir entre las personas que quedan al final, que obviamente son demasiados o proporcionalmente hasta donde se deje llevar. también es de anotar, que se pueden hacer rifas con los artículos y esa manera ayuda a multiplicar el dinero, los terrenos se evalúan mas costosos..en fin. lo digo porque soy Contador Público y a mi manera de analizar el problema, sería una posible solución. porque en mi análisis (ENTRE MÁS ALTO SEA EL PRECIO PARA INGRESAR AL SISTEMA, MÁS GRANDE ES LA OLA QUE SE RETRAE TRAYENDO CONSIGO UN TERRIBLE TSUNAMI) todo mundo va a querer que le devuelvan su monto invertido, y si es alto, mucho mas¡¡ hay mas teorias..
Buena explicación, nada que ver con la lotería donde todo depende de la suerte, o una tanda donde tarde que temprano recibes la misma cantidad de dinero que inviertes.
Aquí se trata de las habilidades que tengas para convencer a otras personas que probablemente no recibirán nada, y la explicación es sencilla cada que recibes dinero habrá 7 personas que no lo recibirán eso te convierte en estafador sin saberlo. Los que pierden como siempre pasa son los que menos saben y pueden ser tus propios amigos y familiares. En pocas palabras estas ganando a expensas de otros con menos habilidades no se ustedes pero yo no podría vivir con eso.
Vivimos en una jungla donde cada quien ve por si mismo y no le importa que los demás pierdan, con un amigo que te ofrezca ser parte de la flor de la abundancia para que quiero enemigos.
Saludos
Yo estoy en un telar y es inigualable las bendiciones que he recibido junto con mi familia y amigos todos super contentos y nadie ha estafado a nadie
Como le hiciste?
Las cuentas están malas, pues asume que solamente la gente entra una vez y al llegar al centro sale y no reinvierte. La realidad es que quien se lo toma en serio reinvierte incluso en su misma flor, los cálculos deben llevar a una flor madre en la que todos los inversionistas generan y reinvierten, alternándose en las flores.
Lee bien. Se explica que, aún si regresaran todos los que han ganado, el sistema no puede funcionar.
Los bancos si no fueran dirigidos por sinverguenzas podrian servir d ejemplo pero resulta que no hacen lo que tu dices bueno si generan dinero pero no para compartirlo contigo sino para arriesgarlo o mal invertirlo por codicia y como ellos todas las aseguradoras,financieras etc son mas piramidales que todos pues la pasta se la quedan 4 para llevarla a paraisos fiscales y las victimas son las personas ahorradoras que escucharon sus cantos de sirena.
Debería estar de más mencionar que es una tontería decir que los bancos son «más pirámides».
En general es un comentario que parece nacer del revanchismo, completamente maniqueo, y en términos generales falso (que no es lo mismo que decir que los bancos no son avaros, o la gente no puede perder sus ahorros en ocasiones).
Alguien me puede explicar exactamente, que son las interaciones?
«Iteración» se refiere aquí a la división en dos de todas las flores vigentes.
Me encantaría que explicaran la fórmula de crecimiento exponencial para poder entenderla.
Entiendo el 8 pero no lo que esta dentro del paréntesis 8. (2 m-1 -1).
Es la cantidad de flores en la iteración m. El 8 simplemente se refiere a que, por cada flor, hay 8 «donadores».
Cómo puedo editar la flor para colocar los nombres?
Buenas estoy organizando algo parecido pero quisiera que nunca fracase que debo hacer para que nadie pierda
No se puede.
SE MANTENER EN EL TIEMPO CON UN NUMERO DETERMONADO DE PARTICIPANTES SIEMPRE AL CUMPLIR LAS 5 ETAPAS CREANDO UN SOLO GRUPO DE CONFIANZA DONDE TODOS GANAN Y NUNCA SE PIERDE COMO ES EL CASO DE LOS BOLSOS DE DIBERO.
Hernan me puedes explicar como lo haces ?? no logro comprenden la idea… y necesito entenderlas urgentemente .