Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
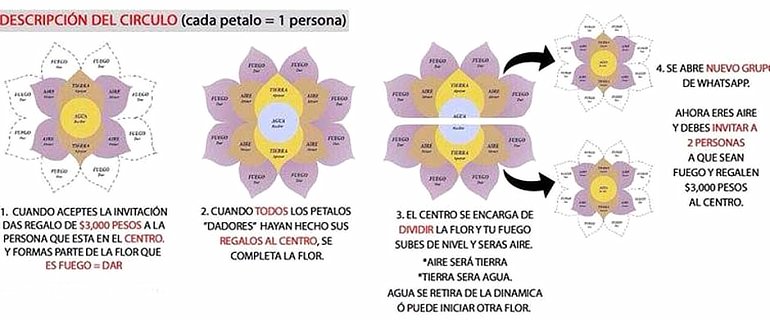
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




SE PUEDE MANTENER EN EL TIEMPO CON UN NUMERO DETERMINADO DE PARTICIPANTES SIEMPRE AL CUMPLIR LAS 5 ETAPAS CREANDO UN SOLO GRUPO DE CONFIANZA CON LAS MISMA PERSONAS DONDE TODOS GANAN Y NUNCA SE PIERDE COMO ES EL CASO DE LOS BOLSOS DE DINERO.
Hola, busco info sobre lo que decis, un numero determinado de participantes. Podes explicarmelo?
Que no te engañe María. Lo que dice es matemáticamente imposible.
Y si las 15 personas colocan el dinero? Me están ofreciendo una donde en teoría las 15 personas invierten, es viable?
Pienso que el problema no radica en el número de personas que se incorporan diariamente (que siempre habrá) sino en el valor de la inversión. Si se comienza con una «poca inversión» (fácil de obtener) es seguro que se encontrarán más personas que quieran invertir y si cada una de ellas invitan a dos el ciclo se irá cumpliendo sin problemas fase por fase hasta la eternidad. Lo que hace difícil que el sistema perdure en el tiempo es la «avaricia» de los que la comienzan imponiendo un monto alto de inversión inicial para ganar mucho, haciendo esto mas dificil a la hora de incorporar mas personas. En el caso que sean 5 fases para una suma de dinero «X» atractiva, esto motivará a las personas a realizar el negocio con ganas y a supervisar y ayudar a los miembros de su flor (15) a seguir creciendo. La única manera de que esto se tranque (haciendolo como debe ser) es que no nascan mas seres en el planeta.
El problema es que no puedes sacar de un sistema más dinero del que metes. Como personas y dinero crecen al unísono con el mismo ratio, nadie JAMÁS podrá obtener más dinero del que metió sin que ello implique dejar a otro sin su propio dinero. Y esto sucede SIEMPRE, bajo CUALQUIER CIRCUNSTANCIA, MECANISMO o FORMA DE ORGANIZARSE.
Hola Hernan, veo que estás empapado en el tema, yo entre en un telar hace dos meses y no he logrado consagrarse porque por el monto de inversión no es fácil conseguir personas que quieran entrar. Tu crees que hay alguna posibilidad de cerrar un círculo y con un grupo pequeño de personas lo repitamos varias veces? Es para no tener que invitar infinitamente a personas.
hola estoy atorada en una, donde te puedo contactar para que por favor me ayudes
No se les debe llamar «perdedores» a los que todavía no han cobrado o realizado su fase inicial donde se recupera su inversión. Estos solo son participantes que cumpliendo los requisitos exigidos por el sistema (invertir y conseguir dos personas) al lograrlo cumplen su turno de cobranza y siguen sin riesgo haber perdido nada.
No entiendes la explicación. Se llaman «perdedores», no porque no hayan cobrado todavía, sino porque JAMÁS COBRARÁN, porque es matemáticamente imposible hacerlo.
Otra cosa mas: no es lo mismo si se ve como un sistema piramidal controlado por una cabeza en un momento determinado (motivación de arranque) que el tiempo lo puede cansar y desmotivar (aunque si se está ganando dinero no tiene porqué cansarse), a que se vea como pequeños grupos de 15 personas controlados o supervisados por la cabeza de ese grupo. Cada vez que se abra una flor o grupo de 15 la motivacion gral de ese grupo crecerá y por ende la de todas las primeras flores o grupo existentes. Además en un sistema (repito) de 5 fases de crecimiento y con una pequeña inversión este debe funcionar facilmente y con efectividad financiera.
¡No funciona! Es imposible que funcione. Deja de estafar a la gente.
Muy claro el artículo!
En mi país hay muucha gente haciendo dinero y lo tienen en secreto.. Ya ellos cerraron el circulo el que está por cobrar vuelve al nivel 4 (se autorecicla) no se cuantas personas se necesitan para que los 15 inicial mas los invitados cobren pero si lo han logrado yo voy a descubrirlo.. Deja de desmotivar a la gente tal vez a estos grupos les tomo meses o años pero lo lograron y están haciendo un buen billete.
HOLA GABRIEL DE QUE PAIS ERES ESTOY EN UNA FLOR DE LA ABUNDANCIA Y YA HE COBRADO 4 VECES SOY DE VENEZUELA ARAGUA SI QUIERES ESCRIBEME Y LE EXPLICO
Hola Vianca
A que email se te puede contactar ? Gracias
04267477619 FLOR DE LA ABUNDACIA Y FLOR DE LA CONFIANZA SE LLAMA
Sirfrave consiguio la solucion
Hola Hernan, veo que estás empapado en el tema, yo entre en un telar hace dos meses y no he logrado consagrarse porque por el monto de inversión no es fácil conseguir personas que quieran entrar. Tu crees que hay alguna posibilidad de cerrar un círculo y con un grupo pequeño de personas lo repitamos varias veces? Es para no tener que invitar infinitamente a personas.
Si tienes 5 manzanas, ¿le puedes repartir una manzana completa a 100 personas diferentes? ¿Verdad que no? Por exactamente la misma razón ES IMPOSIBLE lo que solicitas.
Ya no caigas en la trampa de los embaucadores. Si alguien gana, es porque alguien salió perdiendo SIEMPRE.
Hola Javier, me imagino que debe de ser frustrante explicarle a las personas cómo funciona este fraude y que te sigan respondiendo con cosas que no tienen que ver, no entienden que tarde o temprano este esquema colapsa, o quizás Hernán maneja una flor jajajaj. Buen artículo.
Sobre lo que te dijo en el primer comentario, sí es posible siempre y cuando nadie nuevo entre y nadie salga, al menos así yo entendí: digamos que entre 3 personas acordamos ayudarnos, A y B le prestan a C 100 pesos cada uno, una semana después B y C le prestan 100 c/u a A, y por último C y A le prestan 100 c/u a B. En ese momento los 3 quedaron como empezaron, nadie ganó ni perdió. Agregando más personas es lo mismo, sólo se agrega una ronda más por cada nuevo miembro: 4 miembros 4 rondas de préstamo, 10 miembros 10 rondas de préstamo, etc., lo importante es que nadie entre o salga. Aunque aquí obviamente hay un riesgo muy grande de que el que recibe el dinero se fugue con el dinero de los demás; sólo podría funcionar en un entorno donde haya mucha confianza, casos muy, pero muy particulares.
Gracias por tus palabras.
En el sistema que dices, no hay ganancias como tal. Es un esquema que se parece mucho a lo que aquí llamamos «Tandas».