Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
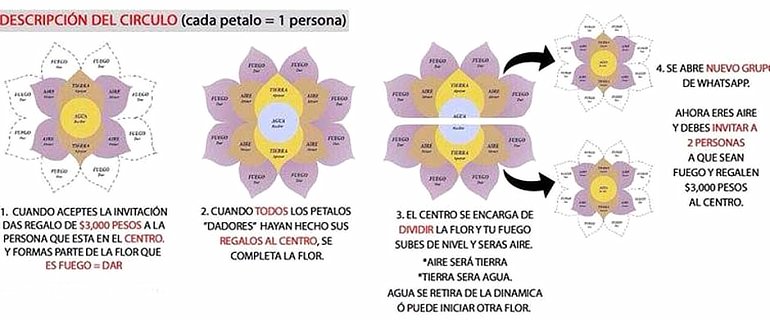
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




Ha sido placentero leer su artículo, fundamentado matemáticamente y sorpresivamente abrumador al ver cuantas iteraciones son necesarias recrear para que todos los participantes «ganen», usted lo menciona como imposible, aunque y por el mismo motivo fue que dí con su articulo es porque yo he visto de su éxito y estoy tentada en entrar a el, claro reconozco que como cualquier inversión se corre un riesgo. Por mi parte deseo investigar y ahondar en el tema lo más posible para así tener una critica o responsabilidad de a lo que me enfrento, este ha sido el articulo mas completo que he encontrado y el que mejor me explica su funcionamiento. Le agradezco su valiosa aportación.
Gracias. Aunque no hay que confundirse. Nunca es posible pagar a todos los inversionistas. Solo recibirán paga la octava parte de ellos SIEMPRE.
Que interesante, pero por ejemplo, que yo ingresara a este sistema, entaria en el ultimo circulo que es fuego. ¿cuantas veces se tendria que dividir la flor para llegar a ser «agua» o llegar al primer circulo o petalo? Una vez estando en la punta de la flor o ser el primero y para que me «Paguen». ¿ Cuantas personas hay que ingresar para recibir el dinero? Gracias
entonses sera mejor entrar ahora a la flor antes de que colapse, advirtiendo a las dos personas que convensas del riesgo que existe
Desarrollé el mismo sistema, pero haciendo en grupo determinado de personas, para que nunca termine y todos tener un ingreso extra. Si se puede. Hablando se entiende la gente.
Cualquiera que entienda la mecánica sabe y entiende (es el propósito de éste artículo) que eso es imposible. Matemáticamente imposible.
Hola francisco, justo estoy rompiendome la cabeza para descifrar cuantas personas necesito para hacer lo q tu dices, q una determinada cantidad de personas cierre ciclo sin meter más gente y q sea permanente me podrás ayudar y decirme cuantas personas necesito?
Francisco miente. La única manera de conseguirlo es hacer un sistema donde NADIE gana un centavo, porque el dinero no se crea de la nada.
Si pretendes crear una flor que «genere ingreso» (léase: le quite dinero a unos para pasarlo a otros) forzozamente necesitas más gente. No se puede de otra forma. Los que tienen más dinero SIEMPRE lo tienen a expensas de otros. ¿Es tan difícil de entender?
El sistema funciona como una forma de financiamiento 1 ganara y 7 perderán perobdonde haya mas flujo esos ganaran más.
Lo interesante de esto es saber por qué le dedican tanto tiempo y atención a explicar e insistir en que no funciona.
No será que alguien tiene miedo de perder el control sobre nosotros y teme que existan otras formas de apoyarnos sin someternos a créditos de interminables intereses?
Lo increíble es que ni la lógica, ni lo matemáticamente inevitable, alcancen para abrirle los ojos.
Si sabe SUMAR, se dará cuenta que se dice que no funciona porque… NO FUNCIONA.
Logicamente es ilogico(jeje) decir que algo que funciona hasta cierto tiempo y que es insostenible sea algo que NO FUNCIONA… Se entiende a lo que quiere llegar con su articulo»fraude colectivo».. Pero no solo son matematicas pues va mas allá de eso; curiosidad, confianza o desconfianza, juego, riesgo, ganar, perder, buenas intenciones, malas intenciones.. Por cierto 1 octavo de posibilidades de ganar en un juego donde participa tanta gente pues le entro al «fraude colectivo» nunca había tenido tantas posibilidades…
No funciona porque no pueden ganar todos NUNCA, además de ser insostenible.
Uno pensaría que el artículo es lo suficientemente claro para que se ENTIENDA que el problema no es ni de confianza, ni de curiosidad, ni cuestión de voluntad, de buenas intenciones o cosas por el estilo.
En otras palabras: 1 + 1 nunca será igual a 4, por mucha buena voluntad, confianza y buenas intenciones que tenga.
Pues mucha matemática !! Pero si funcionan y la gente gana!! Y se produce una abundancia que al sistema bancario no le gusta.
Es un trabajo en equipo y uno gana siempre. A pesar de que uno da un regalo de verdad creeame que recibe 8
No hay pierde lo más que pasa es que tarde un pico más de tiempo.
Pero el aprendizaje que tiene de Confiar ,Dar, recibir , apoyar y trabajar en equipo funciona y es lo más bonito de la flor.
Tomenlo como un curso no como una inversión o tanda.
¡NO! No se gana siempre. ES MATEMÁTICAMENTE IMPOSIBLE.
Uno dice: «no se puede repartir una moneda entre ocho personas». Luego llega usted y dice: «¿Qué importa? Lo que importa es el amor». Pamplinas. La primer razón por la que entra la gente es la ambición. ¿Cómo mantienen su disonancia cognitiva para juntar eso con las tonterías de «dar», «recibir» y «apoyar»? Estafadores egoístas son los que inventaron eso.
Hola pia… te gustaria entrar a una flor ocupo completar gente… porfisss saludos ✌
Ganan los que inician su propia flor y a lo mejor podrán ganar otros pocos más pero eventualmente muchos pierden porque no encuentran personas nuevas. Ojalá todo fuera una cuestión de fe o de buenas intenciones pero no entraste por querer ayudar, sino para ganar dinero.
Hola me gustaria saber que piensas de esta imagen que realice explicando como hay una supuesta ganancia, «perdida»
http://fs5.directupload.net/images/151112/iylmcxhs.jpg
Los siete integrantes interiores de la flor «original» nunca ponen nada. De ahí que esos $7,000 (en flores con «regalos» de $1,000) no existan. Solo paga, como sabes, el nivel 4 que son ocho integrantes.
El problema con tu gráfica, si la entiendo bien, es que estas contando varias veces el mismo dinero. Por eso te parece que debe haber más. Cada flor «genera» $8, 000 no $15,000. Cuando dices $15,000, estás contando de nuevo el dinero de las flores anteriores.
Los únicos que reciben dinero sin pagar nada son los 7 de los tres primeros niveles de la flor «original».
No es posible que aún con una evidencia tan matemáticamente objetiva, insistan en creer que la flor funciona, después no se quejen por el fraude.
De q alguien se va a quedar sin diero es inevitable, las personas que juegan aceptan el riesgo de perder el dinero, nadie los obliga, es lo mismo que en cualquier juego de azar, estos articulos de verdad es para la gente muy ignorante, que no sabe de este tipo de juegos, los que no quieran jugan no jueguen y dejen de estar diciendo pendejadas.
Javier, todo mundo sabe q puede perder el dinero, se llaman riesgos, a nadie se le engaña, cual es tu conflicto con esto?, a ti nadie te esta quitando tu dinero, tu no estas poniendo ningun peso, la gente se sabe cuidar sola y hace con su dinero lo que quiera, lamentablemente hay personas que si quieren fregar a otras pero eso ya es otro rollo. En que te afecta que las personas jueguen esto?????
Mi conflicto es que no es verdad lo que dices. A la gente sí se le engaña. Se le dice que no puede perder, que el sistema es auto-sostenido, etc.
Puedo estar de acuerdo contigo en que la gente es muy boba si entra sin conocer los riesgos. ¿Pero cuánto es el riesgo? Tu mismo, honestamente, ¿tenías presente que hay un ganador por cada siete perdedores? ¿O solo sabías vagamente que «alguien» iba a perder?
Creo que está bien dar los datos duros y precisos. Por otro lado, ¿a ti qué te afecta que yo lo diga?
Definitivamente se que hay un ganador y 7 personas perdedoras, como tu lo dices es logico, yo te apoyo con lo que dices que aveces se les miente a las personas que tienen el 100% de probabilidades de ganar eso ya es cuestion de moral de cada quien, por lo que he visto en esto no conozco algun caso que se le diga a las personas que tienen el 100%, de probabilidades de ganar, que siempre hay riesgo y si quiere jugar adelante y si no nadie lo obliga, y si funciona si no le mientes a la gente, tus comentarios son un negativos acerca de esto al decir no funciona, lo que deverias mencionar es q si se quieren arriesgar adelante pero no es nada malo
No veo por qué te molesta que se pongan las cartas sobre la mesa.
El artículo no es alarmista, no dice mentiras, informa. No grita: «¡no lo hagas!, ¡es una trampa!»¿Para tomar decisiones no se de estar informado? Pues eso.
Si hay que «respetar» la mala moral de cada uno, también habrá que respetar la buena, supongo.
A mi me parece muy bien tú explicación, si a vemos gente que ignoramos este método y es importante que encontremos información adecuada y sobre aviso no hay engaño. El que es tranza es tranza :-) .