Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
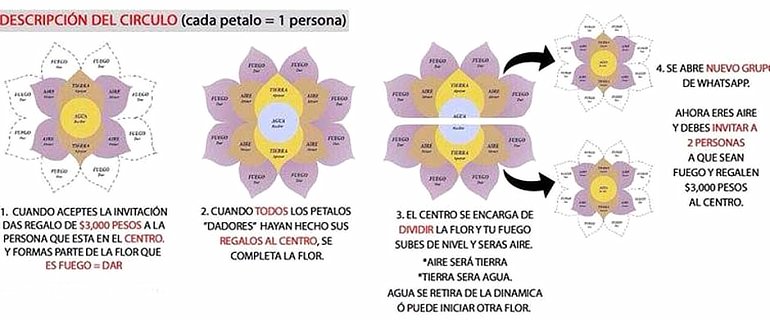
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




Javier, celebro tu paciencia y tu buena intención por explicar este fraude, yo hubiera llamado más que idota a algunos cuantos.
Cuando alguien quiere pelear contra los números, no hay nada que hacer, no existe explicación o evidencia suficiente para sacar de su error a ese ente o para hacerlo dejar de mentir, dependiendo de la posición en que se encuentre.
Excelente artículo Maestro,explica de forma muy simple y con bases científicas este famoso asunto de la flor de la abundancia.
This is like a disease that is eating away at my little town. The people have gone crazy. Loco for money. Some will win some will lose. They will not listen. They even ask us not say negative things about it so they can con on other people. It’s horrible and it’s not stopping it’s getting worse. And posting your article for which I am very grateful and hope that they will wake up to the reality.
Excelente Articulo.
No es cierto, aquí no están Exponiendo que cuando uno gana vuelve a entrar debajo de quienes le dieron…. Pueden explicarlo con matemáticas así???
No entendí esta parte, la podrías explicar tu, aunque no sea con matemáticas
Te lo explico con manzanas (literal):
Imagina que formas en una fila a 100 personas, cada una con una manzana. Cada una la deposita en una caja.
Ya que pasaron todos se vuelven a formar y cada uno toma 8 manzanas. La pregunta es: ¿A todos les van a tocar 8 manzanas? Obviamente no. Se acaban antes. Para que les toque a todos los que ya echaron su manzana nuevas personas tienen que echar una manzana (muchas más personas cada vez). Para que a esos nuevos les toque manzana hay que llamar a más y así. Como no hay un número infinito de gente, tarde o temprano la cosa se cae, con mucha gente (7 de cada 8) sin manzana.
No importa si los que ya tomaron una manzana se vuelven a formar y echan otra. No pueden alcanzar para todos. La única forma de que todos tengan manzana es que sólo tomen la manzana que echaron antes. Es decir, sin ganar nada.
El orden en que pasen las cosas o el nivel en que entren a la flor es irrelevante.
¿Se ve así lo estúpido que es todo?
Bueno si lo piensas si lo esta explicando solo tienes que introducir ese 1 que esta entrando y reducirlo al numero final de la interacion lo cual termina siendo un % mínimo ya que dependiendo se los niveles siempre sera la proporcion de elnivel ganador x elniver perdedor ( inversión)
Obviamente es la famosa pirámide invertida de todos los tiempos lo preocupante es la corta memoria y como experimento es muy interesante saber que siempre existen ingenuos (tontos) y listos (vividores) en todo ámbito de la vida
Hola Javier, interesante este sistema es como una forma de ganar dinero sabiendo que en algún momento alguien perderá, yo creo que la ambición es infinita y el sistema es sostenible las primeras iteraciones, después de eso me queda claro que esto se sale de control.
Apesar de tu explicación, no es tan sencillo entenderlo una vez que te proponen entrar. No solo se trata de matemáticas si no de conciencia ..difícil incluso opinar en esto pero demasiado interesante como para no opinar, viendo que respondes XD
PD No se si se publico bien mi mensaje
Lo mismo pueden explicar con el gobierno para que tantos senadores ganando tanto dinero al año? Para que el pueblo entero lo entienda como es que generan tanto, todos están preocupados por la dinámica de la flor de la abundancia pero el gobierno hace cosas peores y no las investigan a fondo no les sacan las matemáticas igual, no quiere decir que estoy a favor de la abundancia lo aclaro.
Javier, muy interesante tu explicación, me gustaría que realizaras un análisis de un sistema llamado «Instanmoney» lo pues buscar en youtube. Agradezco de antemano tu respuesta y te envío un cordial saludo.
Gracias por tus comentarios.
Respecto a InstanMoney, el sistema esencialmente es el mismo (se requiere cada vez de más personas para cubrir la inversión inicial de cada persona que entra). Aunque el orden y manera de hacer las cosas varia el problema es exactamente el mismo: el mundo no es infinito y debe caer tarde o temprano. No hace falta entrar en particularidades. Ambos son sistemas piramidales, aunque éste último es un poco más enrevesado.
Las pérdidas se reparten entre más personas, siendo las pérdidas individuales un poco más pequeñas (el sistema habla de $100). Pero crece bastante rápido el número de personas. Seguramente los fracasos son constantes y mucha gente que da sus $100 no los ve. Pero como es poco no lo sienten tanto. Ojo: realmente la gran mayoría de la gente no recibe sus $100 de vuelta.
No hace falta entrar en particularidades.
Hola Javier
Excelente articulo.. Queda muy claro que hay un riesgo en no recuperar la inversión si no eres de los inversionistas iniciales. Me pregunto si el sistema de pensiones del gobierno funciona con este modelo? Siempre he tenido la impresión que llegará el día en que no habrá suficiente dinero para pagar las pensiones si la tasa de empleados disminuye o las aportaciones de los trabajadores no son suficientes. Qué opinas?