Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
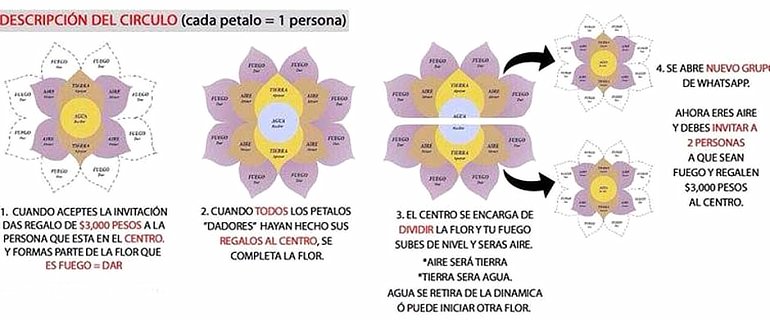
¿En qué consiste la flor?
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




Si por privilegio se entiende, en su sentido propio y original, un Estado que garantiza y protege derechos disponibles para algunos y no para otros.
La concepción (dominante) en la mayoría se utiliza como justificación para rechazar al (innovador) individual.
No es innovación ni como estafa.
Las flores son un sistema que ya se ha aplicado en muchos países con las consecuencias que ya sabemos: se acaba la fiesta porque es matemáticamente imposible que no se acabe.
Si tanto le entiendes a Economía. Deberías entenderle a esto.
Saludos
Richys, Richys. Mira:
Si el hecho de que uno de cada ocho va a ganar dinero significa «funcionar», entonces funciona. Se que no te parece que sea así, porque esos 7 que no ganan son los del final, cuando todo el sistema se cae. Se juntan tantos por el crecimiento exponencial del sistema.
No importa que reinviertan los ganadores. Eso ya está explicado en el artículo. Aún así el sistema es insostenible por largo tiempo. Léelo de nuevo y entenderás porque.
Entiende que los ganadores son ganadores porque le están quitando el dinero a otras personas, y mientras más lejos se llegue, más personas perderán su dinero. Eso debe pesar sobre la conciencia de los ganadores, por lo menos.
No es una opinión, es una realidad matemática. Punto.
El discurso sobre los bancos y las ratas del gobierno está de más. Son ratas, pero eso no hace que las flores funcionen indefinidamente.
Un saludo.
AMIGO…tus cuentas estas bien al igual que mal.. tus cuentas los basaste. … en una persona por flor y ese es tu error
Corrijo (por petalo)
Una persona puede invertir tantas veces le sea posible … osea que esto no acaba .. todos ganas
Amigo.
El que los ganadores reinviertan siempre ya esta contemplado. Aunque reinvirtieran en más de un pétalo. AÚN ASÍ es insostenible. Entiende que los ganadores no alcanzan para «tapar» los lugares nuevos. NO PUEDEN ALCANZAR.
Sigue el razonamiento del artículo y entenderás porque.
Desde el pasado.. hasta ahorita se han creado nuevos sistemas finanzieras y así será siempre
Te reto a crear un sistema de flores que funcione en tu casa. Inventate las personas y el dinero. Usa frijoles por dinero si quieres. Si quieres modifica el sistema y que sean solo 3 niveles de pétalos. Como un juego. Haz que reinviertan, todo lo que tu crees que funciona. Házlo.
Verás que el sistema tendrá que parar porque siempre necesitarás más gente (y frijoles). Ninguno es infinito, y saldrán perdiendo en la proporcion de pétalos que tengas en el ultimo nivel.
Me sorprende tu gran capacidad de tolerancia, paciencia o vitud para hacer entender a Richys, por favor dejalo seguir creyendo en la Ley del minimo esfuerzo, tiene que defender su postura de otra manera no conseguira sus victimas para «cerrar su flor»
Mi novia no le llama «tolerancia, paciencia o virtud». Le llama «ser terco». XD
De echo.. sigo en eso viendo los avances
En alalgunos el problema es las redes sociales y comentarios negativos haciéndoles fracasar
En frijoles de ejemplo es obvio.. una semilla no puede proporcionar más semillas es lógico
La semilla da mas semillas si las plantas y las riegas, las semillas no producen semillas por buenas intenciones, los billetes dan mas billetes si se trabaja y se proporciona un valor, loa billetes por si solos y por pura buena voluntad no pueden proporcionar mas billetes, es lógico
Excelente artículo, veo que muchas personas no comprenden lo simple del sistema y su incapacidad de ser sostenible.
Yo por mi cuenta no he entrado a estas flores una porque el riesgo, aunque no lo veamos es grande, y otra porque hay que tener conciencia de que habrá personas perjudicadas al final de la cadena.
Saludos!