Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
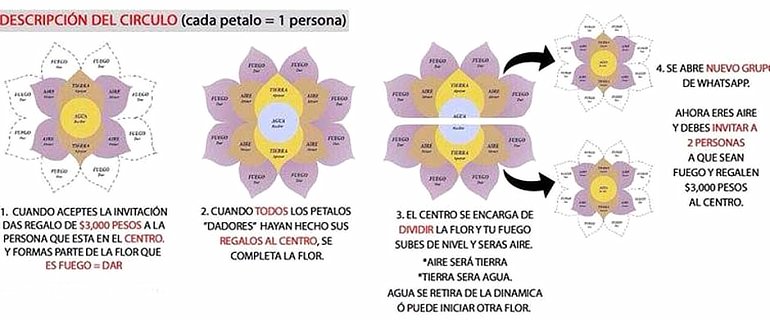
¿En qué consiste la flor?
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




SI CADA UNO ENCUENTRA OTROS DOS INVERSIONISTAS LA FLOR NO COLAPSARA, Y NO ES FRAUDE, FRAUDE CUANDO UNA PERSONA ES LA QUE MUEVE EL DINERO Y SE APROVECHA DE LOS DEMAS, COMO PASA EN EL WATSAP Y EN REDES SOCIALES. AUNQUE ES CLARO QUE UNO SE BENEFICIA A COSTA DE LOS DEMAS Y ELLOS DE LOS DEMAS Y ASI CONSECUTIVAMENTE, EL TRUCO DE LA FLOR SE ESTANCA CUANDO LOS QUE DAN EL DINERO NO SE MUEVEN PARA BUSCAR MAS INVERSIONISTAS. YO CREO HABER ECONTRADO UNA FORMA DE QUE LA FLOR NO COLAPSE CON 61 PERSONAS.
Hola saide, me interesaria conocer tu teoría… me la podrías explicar?? Te dejo mi correo…
Messico_italiano@hotmail.com
Amigos.
Lamento informar que la presunta solución de SAIDE no existe ni puede existir, como no existe 2+2=5. Él los engaña o se engaña a sí mismo.
Así son las leyes de las matemáticas, qué le vamos a hacer.
exacto, como dijiste, siempre crece mas rapido el numero de invercionistas que los que se reintegran
buenas tardes saide me interesaría conocer tu forma de manejar la flor con esas pocas presonas me es muy necesario para la flor donde estoy no colapse te agradecería mucho gracias. ahí esta mi correo retrox_18@Hotmail.com
Ya te mando Saide su teoría??
Yo te voy a explicar la teoría:
Imagina que hay 100 personas con $1,000 en la cartera cada una para invertir en las flores (suponiendo flores de mil pesos). Si sumamos el dinero de todos tenemos $100,000. ¿Va? Ok.
Para que todos ellos resulten ganadores deberían tener al final $8,000 cada quien. Es decir, juntando los $8,000 que gana cada uno serían $800,000. Pero, ¡ay!, ya dijimos que sumando el dinero de todos tenemos tan solo $100,000. ¿De dónde van a salir los $700,000 que faltan para pagarles a todos?
Forzosamente tiene que salir de gente que venga de fuera. Más gente. ¿Y quién le va a pagar a esos nuevos? Pues más gente, y así, ad infinitum. Pero como la gente en el mundo no es infinita, el sistema tiene que parar forzosamente.
¿Qué parte de insostenible e imposible no se entiende? No existe el sistema de Saide. No puede existir.
Hay 7 mil millones de personas en el mundo….. Hay 7 mil millones de posibilidades…
De las cuales como 6 mil millones se quedarían sin «premio».
Estoy de acuerdo contigo hermano, pero déjalos creer en una posibilidad inexistente que les provoca una paz interna. La cual terminará cuando la flor marchite jeje
Es tan pero tan obvio que es un fraude que no entiendo cómo no se dan cuenta
Hola, saide, me interesa tu teoria para que no colapse la flor, me la puedes explicar porfavor, te dejo mi correo
HOLA ME GUSTARIA SABER PARA QUE LA FLOR NO COLAPSE TU PROPUESTA GRACIAS
TE DEJO MI CORREO KZ_TILLO@HOTMAIL.COM
HOLA SAIDE ME INTERESA TU METODO ME PODRIAS EXPLICAR TE DEJO MI CORREO, MIL GRACIAS
hola saide me puedes explicar. es que me invitaron se que me tocara por wue ya tengo gente abajo. pero me preocupa tambien la gente que esta mas abajito
Saide explicame eso de evitar el colapso con 61 personas !!! Saludos !!!
Hola Saide, me interesaría saber tu propuesta para que no colapse la flor de ante mano muchas gracias
Hola me interesa saber tu río para q la flor no colapse y si fuera posible q no se parta en 2
Te paso mi correo esperó me ayuded xfavor
Rtapia173@gmail
Javier, es «refrescante» poder contar con voces como la tuya que se pronuncien a favor de la razón y del pensamiento crítico. En general estoy a favor de tu planteamiento, pero te agradecería pudieses apoyarme a esclarecer un punto: ¿cuál es el número de gente sin cobrar en un momento dado del tiempo (llamémosles perdedores)? Y es que no es lo mismo que «inversionistas» porque a partir de la tercera iteración algunos inversionistas también son ganadores. Mi conclusión es que por cada 15 ganadores (asumiendo que los 15 participantes de la flor original logran cobrar) hay 112 perdedores (14 x 8) para un total de 127 personas distintas envueltas a la tercera iteración. Me interesa la fórmula para calcular tanto el total de personas envueltas como el número de perdedores dada una iteración. ¡Felicidades, saludos y gracias!
Hola.
Si entiendo bien tu pregunta, lo que deseas saber es cuántas personas se encuentran en el sistema en una posición que no les permite cobrar. Es decir, aquellos que no son el centro de las flores existentes. ¿Es así?
Si es así, la formula es simple: existen siempre 14 pétalos en cada flor que no son el centro. Como el número de flores se duplica en cada iteración, el número de pétalos que no están cobrando es siempre 14 x (el número de flores). Es decir, para la iteración i existen:
pétalos que no cobran = 14(2^i)
Este es el número máximo de personas que no están en posición de cobrar en la iteración i (asumiendo que se han juntado los ocho inversores para todas las flores existentes, pero aún no se consideran como «cerradas»). Pueden ser menos porque es posible que una persona utilice más de un pétalo a la vez, o bien existan re-inversores.
Pero los re-inversores máximos son muy pocos. En la iteración i tan solo pueden ser (2^i)-1. Que es la cantidad de flores construidas con anterioridad, cerradas y pagadas, que ya no existen en la iteración i. Es decir, una catorceava parte del total de personas en el sistema en posición de no cobrar.
Gracias Javier, el mejor articulo que he leído a cerca de la Flor de la abundancia. Saide, es importante tu aportación te lo agradeceré. mht0290@gamil.com
SAIDE M INTERSA SU APORTACION YA QUE SERIA DE GRAN AYUDA PARA MUCHOS T DEJO MI CORREO, estoy en un grupo con mas de 150 personas
delhy2786@gmail.com
A mi también Saide mándame tu teoría xfis…
oskrin_17@hotmail.com
Vamos! Todos sabemos que la persona que empieza con esta dinamica de «abundancia» no invierte mas que el tiempo de pensar en nombres para los petalos!
La persona del boton recibe su dinero sin invertir un solo peso ya se parte y el boton se va bien alegre con 4000 pesos supongamos. Bueno mi pregunta es si en algun moment ya nadie quiere participar los petalos morados salen perdiendo? O como es esto no tiene fin? No entiendo supongamos que nadie en el mundo quiere participar los que invirtieron 500 pesos los pierden espero entiendan la pregunta porque para mi esto es lo mas falso que exista. Seria preferable una tanda aunqur tampoco es confiable pero hay si todos invierten y reciben despues de cierto tiempo dependiendo del numero que toco.
Buen dia ;)
Muy bien explicado y no entiende el que no quiere entender, desde que a mi me invitaron a participar dije que no por una sola razón: es ilógico que te den más cantidad de la que inviertes una sola vez. En donde yo vivo se ha vuelto una moda, lamentablemente tarde que temprano se hará una revolución por los que no recibieron su dinero, pero nadie más que ell@s tendrá la culpa por no pensar las cosas dos veces.
Me cuesta trabajo creer q colapsa. Sin embargo como me dijo un lider de multinivel retirado… Una red que no desplaza un producto o servicio se cae.
Colapsa porque cada vez se necesita más gente, en forma exponencial (entender eso de «exponencial» es muy importante). Y básicamente la cantidad de gente en el planeta Tierra no es infinita. Y no hay forma NO HAY, de darle vuelta a eso. Por esa simple y llana razón.