Alguien te promete que al invertir 3 mil pesos (o euros o dólares, o lo que tu quieras), recibirás de regreso 24 mil. ¿Tiene esto sentido? Aquí están las matemáticas de «la flor de la abundancia».
Si te cuesta trabajo seguir las fórmulas, visita: Flores de la abundancia… ¡con manzanas! para una versión en texto, fácil de seguir.
Un breviario
En la flor es más probable ganar que en algunos juegos de casino, aunque siempre a costa de muchos otros. Por cada ganador hay, en promedio, siete perdedores SIEMPRE. No tienen que ser de la misma flor que los ganadores, ni estar cerca en el tiempo o espacio a los mismos. Pero existen y son inevitables.
Vender la idea de que es algo seguro y sostenible es faltar a la verdad y un profundo engaño y estafa. Entrar es una decisión ética y moral de cada uno.
Lo que no es la flor:
- Una alternativa a los bancos (o la economía moderna)
La realidad es que es un mecanismo que mueve el dinero de muchos a las manos de unos pocos (los ganadores). No fomenta una equitativa distribución de la riqueza, sino todo lo contrario. - Un sistema sostenible
Es matemáticamente imposible sostener la flor de manera indefinida. No es una cuestión de voluntad, ánimo o ganas. Es matemáticamente IMPOSIBLE. Y sobre esa imposibilidad trata este artículo.
¿En qué consiste la flor?
Se forma un grupo de 15 personas repartidas en 4 niveles diferentes:
- Una en el primer nivel (el que recibe el dinero).
- Dos en el segundo nivel (el nivel de «apoyo motivacional»).
- Cuatro en el tercer nivel (el de aquellos que invitan a nuevos integrantes).
- Ocho en el cuarto nivel (el de los recién llegados y aquellos que ponen el dinero).
Cuando todos los integrantes del cuarto nivel han «regalado» su dinero, la flor se considera completa. El dinero es recibido por el individuo del nivel uno, que para llegar ahí tuvo que pasar (presuntamente) por todos los niveles anteriores. Él se retira, dividiendo la flor en dos nuevas, colocando a los integrantes originales en el nivel de numeración inferior al que poseían en la original.
Ambas flores carecen del último nivel que tienen el encargo de poblar, y la única forma de hacerlo es consiguiendo nuevos «inversionistas» que donen su dinero al nivel uno de sus respectivas flores. Y así, ad infinitum.
Bueno, ad infinitum no, porque el mundo no es infinito.
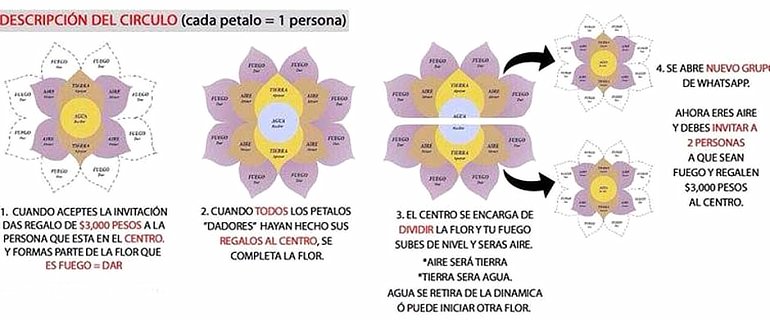
¿Cómo crece el número de personas necesarias?
En otras palabras: ¿a qué velocidad crece el número de personas necesarias para sostener la dinámica?
Imaginemos que solo existe una flor. La flor original. Olvidemos cómo llegaron los integrantes a cada uno de los niveles. Simplemente tenemos un grupo de 15 personas, 8 de las cuales han donado su dinero.
Inversionistas = 8
Ganadores = 1
La flor se divide en otras dos que necesitan, cada una, una tanda de 8 personas. Es decir, que se necesitan 16 personas en total. Con las flores ya completas y contando a la anterior, tenemos:
Inversionistas = 24
Ganadores = 3
Estas dos nuevas flores se dividen, creando 4 flores en total. Es fácil darse cuenta que los números se actualizan como sigue:
Inversionistas = 56
Ganadores = 7
En general, el número de inversionistas para m iteraciones del sistema (entendiendo como «iteración» la división de todas las flores vigentes) crece a la misma velocidad exponencial que el número de ganadores, porque en cada iteración se doblan. Pero el número de inversionistas siempre es mayor en un factor de 8, porque fueron más al principio.
El crecimiento de los inversionistas, para m iteraciones del sistema sigue la siguiente regla:
\displaystyle \sum_{n = 0}^{m} 2^{3 + n} = 8(2^{m + 1} - 1)
Mientras que el número de ganadores crece de la siguiente forma:
\displaystyle \sum_{n = 0}^{m} 2^{n} = 2^{m + 1} - 1
Como debe resultar evidente al observar las expresiones derechas, el número de ganadores es una octava parte de los inversionistas.
En otras palabras: la proporción entre ellos es siempre de 8 a 1, que es precisamente la proporción de la ganancia respecto a la inversión (si por ejemplo inviertes 3 mil ganas 24 mil. Que es lo mismo que 3 x 8 = 24).
Es decir, al ganar recibes los 3 mil que habías invertido y 21 mil de inversores distantes que probablemente jamás recuperarán su dinero, porque el dinero no se crea de la nada, y si alguien tiene más al final, es porque otro tiene menos.
Puede ganar mucha gente, pero los perdedores serán 7 veces más por lo menos. Esto asume que el dinero se regresa a los inversores de la última capa si la flor no se cierra. Los perdedores pueden ser muchos más si no es el caso.

Si los ganadores anteriores se reintegran al juego, ¿no se compensa el crecimiento de los inversionistas?
No importa mucho que se reintegren al juego, porque el número de inversionistas crece mucho más rápido. Imaginemos que el sistema completo ha alcanzado las 10 iteraciones. Esto nos da un total de «inversionistas» de 16,376:
8(2^{10 + 1} - 1) = 16,376
Mientras que el número de ganadores con el dinero en la mano hasta la iteración anterior ascendería tan sólo a 1,023:
2^{9 + 1} - 1 = 1,023
Como es obvio 1,023 ganadores no alcanzan para cubrir a los 16,376 inversionistas necesarios para completar la siguiente iteración. Siempre tiene que ingresar gente externa y siempre cada vez más.
¿Por qué cae el sistema?
Lo presentado con anterioridad es una versión simplificada del comportamiento global, que se puede complicar tanto como se desee. Siempre puede haber personas que inviertan en muchas flores a la vez, que usen más de un «pétalo» al momento de ingresar al juego, etc. Pero lo expresado arriba captura la esencia de la dinámica y el comportamiento que domina el sistema: el crecimiento exponencial. Ese crecimiento dominará siempre y por completo cualquier intento por minimizar sus efectos. Es imposible que no sea necesario agregar más personas de las que había anteriormente. Y además, cada vez más (el doble o casi el doble cada vez).
El sistema cae porque llega un momento en el que es imposible (no difícil ni arduo: imposible) conseguir más personas que ingresen a él.
Al momento de llegar a un número de iteraciones tan modesto como 20, el sistema habría necesitado 16,777,208 inversiones. Número que equivale casi a la cantidad de habitantes en el área metropolitana de la Ciudad de México. Y sí, para realizar una sola iteración más, ¡se necesitaría ese número de personas nuevas! Es evidente que el sistema caerá mucho antes de llegar tan lejos.
Cuide su dinero.




… entonces los autorizados y legalizados para crear una pirámide son:
Nivel 1-fabricante. Nivel 2-distribuidor regional.
Nivel 3- distribuidor nacional. Nivel 4 minoristas y NIVEL-5 LAS MASAS-CONSUMIDORES. esto me cuesta mas trabajo de aceptar y mas aun que al banco le des tu dinero en ahorro por un misero 5% anual y que el banquero lo preste en tarjeta de credito al 40% anual. Vaya sistema. Peor el q lo acepta. Gracias Mano Invisible de la Oferta y Demanda.
Lo que hacen los personajes que mencionas no son pirámides. No mezcles churros con merinas. Creo que tu interés es sincero, pero considero buena idea que te informes de fuentes serias y hasta académicas, sobre la naturaleza y funcionamiento del sistema económico, la bolsa, etc.
Por su incomprensión (de eso y la más elemental de las matemáticas), la gente cae en la trampa de las flores y pirámides, al grado de no entender porque colapsan forzosamente.
Hay pero si ariesgas 1000 pesos tampoco se te acabara la vida no ?????? Osea es lo q te gastas en un dia de peda , por q no ariesgar , si los pierdes es igual q loa hubieses perdido en una fiesta y ya …….. el q no ariesga no gana bueno eso digo yoooo , lo hare y despues les platico como me fue :)
Por esa manera de pensar es que las flores tienen tanto exito, seguira siempre que alguien (14) este dispuesto a perder su dinero, y mantener a los botones, pero esos botones en algun momemto perderan y perderan y dejaran de apostar a seguir perdiendo. Prefiero gastar mis mil pesos que regalarlos.
miren chavos no es necesario ser un gran matemático para saber que muchas personas saldrán perdiendo. para que una flor este completa se necesitan 15 personas de las cuales 1 sera la beneficiada. completada la flor se separa y se hacen 2 flores por ende dos beneficiados mas, pero ahora participan 31 personas.
ya han participado 31 personas distribuidas en solo 3 flores generadas de la original, donde solo se han beneficiado 3 personas. alguien sabe cuantas personas deben participar para que las 28 personas restantes se beneficien? la respuesta es aproximadamente 255 personas. y si seguimos las cantidades aumentan considerablemente y no dejaran de aumentar, como ya comentaron es infinito.
Me parece increíble la forma en que se puede llegar a manejar este sistema. y también existe la posibilidad de que todos ganen y incluso que la flor se cierre sin que alguna persona que de dentro sin ganar.
Magnífico artículo, y me parece increíble que algunos de los comentarios insistan en que el sistema es sustentable. Me encantan las matemáticas, gracias por ilustrarnos.
La explicacion que nos dieron arriba es muy censilla, recuerden que nadie dá dinero gratis. Todos los que dicen que si funcionan quieren dinero fácil y la verdad hacer dinero cuesta y mucho. Esa teoria les cae muy bien a los ilusos que creen que todo lo obtendrán fácil (No se dejen engañar, busquen siempre la verdad, pues la mentira siempre genera problemas).
Me parece que esto es como las maquinas de «movimiento perpetuo» que en teoria despues de darles un impulso, reciclan la energia para que la maquina se sigua moviendo infinitamente. En teoria es posible, pero en la practica todas estas maquinas se acaban por deterner pues hay por mas eficiente que sea la forma en que se «reciclala energia», siempre habra una perdida, por minima que sea por la friccion con el mismo mecanismo de la maquina y el aire que la rodea. No soy experto en matematicas, pero me parece que es algo similar, se recicla el dinero y para que siga habiendo dinero se le debe administrar mas dinero, como a la maquina mas energia para que siga moviendose.
Hola Javier tu explicación fue muy clara y sencilla de entender, a todas luces no hay manera de ganar. Mi comentario es xq en mi cd. Se a presentado una nueva modalidad de flor y me gustaría que me ayudaras a descubrir donde esta la trampa ;) en esta modalidad vamos a decir entras con 1000 y recibes 8000 que a la hora de cobrarlos te piden que dejes 1000 a la flor para «reembolsos» cuando la flor se apage y devolverles su dinero a los que no alcancen a cobrar, Crees que sea una buena solución? Me interesa tu respuesta muchas gracias de antemano
Hola Patty.
Aunque no me queda claro quién se queda con los $1000 que se regresan, el caso es el mismo. El reembolso es mucho más pequeño que lo invertido. Si te entiendo bien, serían $1000 por cada $8000 invertidos. Se paga a uno. Es como si la última capa de la flor tuviera 7 pétalos y no 8. Por lo demás es lo mismo.
Gracias x tu rapida respuesta, Los 1000 que se dejan a lo que yo comprendo es a la persona que organiza, entonces lo que yo entiendo es que x cada ciclo cumplido el organizador gana 8000, que no vuelven a la flor, o estoy mal? Si este logra sacar 3 o 4 ciclos antes de que tenga que «reembolsar» se llevaría una buena ganancia sin siquiera invertir un peso
Saide me podrias proporcionar info. Mi flor puede colapssr envia por favor tu teoria a mi correo martr2004@hotmail.com
hola voy a asistir a una platica de un movimiento similar solo que son 24mil y recibes 192mil me imagino que es como todo lo anterior por que me dijeron que tendria que reservar 48 mil de los 192mil recibidos.
IGUAL A MI ME INVITARON A UNO DE 24 MIL PERO NO LE QUIERO ENTRAR
DE DONDE ERES???